Neural Network Tutorials - Herong's Tutorial Examples

∟RNN (Recurrent Neural Network)

∟RNN Recursive Function

This section provides a quick introduction of RNN (Recurrent Neural Network). It starts from a generic neural network hidden layer, and slowly converts it into a RNN layer by combining the weighted average with the activation function into a recursive function to manage a feed from one sample to the next sample recursively.

From previous section, we learn that a RNN layer requires a recursive function R() that takes two inputs and generate two outputs. One output, called y, goes to the layer and the other output, called s, stays in the same layer and is used as an input the next sample.

In this section, we will learn how to construct the recursive function R().

A simple option to construct the recursive function R() is to set the state vector, s_t, to be the same as the output vector, y_t. And use an activation function as the recursive function with input extended to take both inputs x_t and s_t-1:

Generic form:
  (yt, st) = R(xt, Wt, st-1, Ut)

Simplified form:
  yt = f(Wt·xt + Ut·st-1)
  st = yt

Or:
  yt = f(Wt·xt + Ut·yt-1)

Or:
  yt = f( |Wt, Ut| · |xt  | )
        (            |yt-1| )

f() represents the activation function, same as traditional neural networks.

· represents the dot operation of a matrix and a vector.

The above recursive function become different variations with different activation functions:

f() = sigmoid():
  yt = sigmoid(Wt·xt + Ut·yt-1)

f() = tanh():
  yt = tanh(Wt·xt + Ut·yt-1)

f() = ReLU():
  yt = ReLU(Wt·xt + Ut·yt-1)

...

If this simplified recursive function model is used, a RNN cell (actually a RNN layer) can be illustrated in different diagrams. Here are some examples I have collected from the Internet.

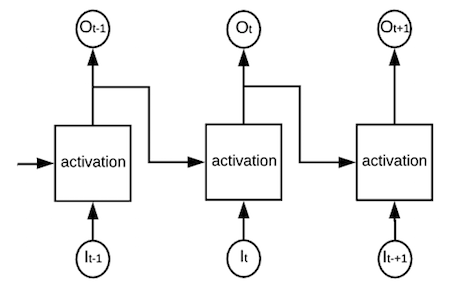
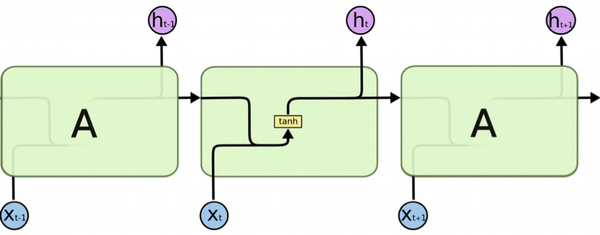
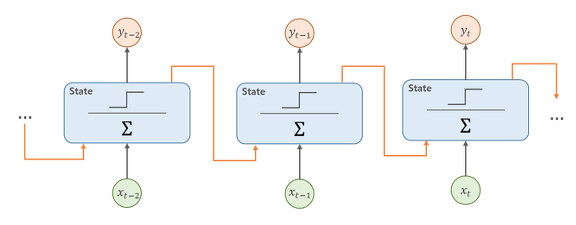
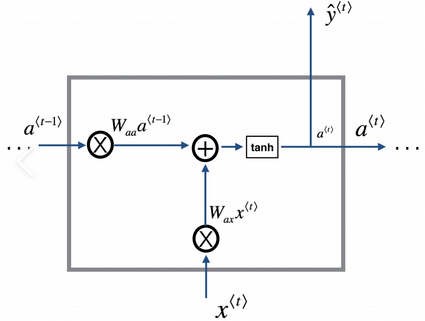
Table of Contents

 About This Book

 Deep Playground for Classical Neural Networks

 Building Neural Networks with Python

 Simple Example of Neural Networks

 TensorFlow - Machine Learning Platform

 PyTorch - Machine Learning Platform

 Gradio - ML Demo Platform

 CNN (Convolutional Neural Network)

►RNN (Recurrent Neural Network)

 What Is RNN (Recurrent Neural Network)

►RNN Recursive Function

 What Is LSTM (Long Short-Term Memory)

 What Is GRU (Gated Recurrent Unit)

 GNN (Graph Neural Network)

 GAN (Generative Adversarial Network)

 Performance Evaluation Metrics

 References

 Full Version in PDF/EPUB

RNN Recursive Function - Updated in 2023, by Herong Yang