Physics Notes - Herong's Tutorial Notes - v3.24, by Herong Yang
Elapsed Time between Distant Events
This section provides a thought experiment to demonstrate that elapsed times between two events that happen at different locations in a moving frame may be observed as contracted or dilated from a stationary frame.
If you review the thought experiment presented in previous sections carefully again, you will notice that the two events Amy selected to synchronize her clock are happening at the exact same position in her reference space:
- Event A - Light pulse leaving the laser meter.
- Event B - Light pulse coming back to the laser meter after reflected from the mirror.
This is a very important condition for deriving the time dilation phenomenon. Without this condition, we could derive some contradictory conclusions. Let's consider a slightly modified thought experiment as an example:
Part 1 - Amy on the Train:
Amy turns the laser with a backward angle, which is precisely calculated so that when Bob observes the light pulse on the ground, it travels straight up vertically.
Amy also moves and turns the mirror so that light pulse is reflected back to the laser meter.
Amy considers 3 events in the experiment:
- Event A - Light pulse leaving the laser meter.
- Event B - Light pulse reflecting at the mirror.
- Event C - Light pulse coming back to the laser meter after reflected from the mirror.
Amy establishes the relation of the elapsed time T of her clock with the distance between the laser meter and the mirror L:
L = c*T (T.23) - Amy's observation # L is the distance between the laser meter and the mirror # T is the elapsed time between events A and B # T is also the elapsed time between events B and C
Part 2 - Bob on the Ground:
When Bob observe Amy's experiment on the ground, he will establish the following relations:
L' = c*T' (T.24) - Bob's observation events A and B # L' is the distance between events A and B # T' is the elapsed time between events A and B L" = c*T" (T.25) - Bob's observation events B and C # L" is the distance between events B and C # T" is the elapsed time between events B and C
Part 3 - Contradictory Conclusions:
Using geometric relations of L, L' and L", we can derive the following conclusions:
L = c*T (T.23) - Amy's observation L' = c*T' (T.24) - Bob's observation events A and B L' < L (T.26) - geometric relation T' < T (T.27) - merging T.23 and T.24 into T.26 # Amy's clock is faster between events A and B! L" = c*T" (T.25) - Bob's observation events B and C L" > L (T.28) - geometric relation T" > T (T.29) - merging T.23 and T.25 into T.28 - Amy's clock is slower between events B and C!
Something went wrong with thought experiment. But I don't know where.
In order to avoid this problem, we probably should modify the time dilation definition with extra condition as: "The elapsed time between two events that happen at the same location in a moving frame is dilated when observed from a stationary frame."
With this definition, we can easily derive the following statement: "Time on a moving clock is dilated when observed from a stationary frame." because clocks are always using events that periodically happen at the same location in their own frames. Think about old swing clocks.
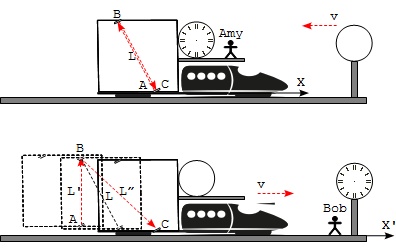
Table of Contents
Introduction of Frame of Reference
Introduction of Special Relativity
►Time Dilation in Special Relativity
Time Dilation - Moving Clock Is Slower
Demonstration of Time Dilation - Amy on the Train
Demonstration of Time Dilation - Bob on the Ground
Demonstration of Time Dilation - Formula
►Elapsed Time between Distant Events
Length Contraction in Special Relativity
The Relativity of Simultaneity
Minkowski Spacetime and Diagrams
Introduction of Generalized Coordinates