Demonstration of Time Dilation

∟Demonstration of Time Dilation - Bob on the Ground

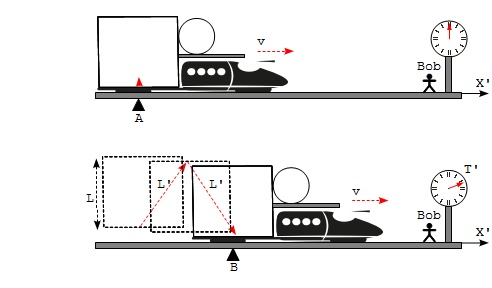
This section continues the thought experiment to demonstrate time dilation with Bob observing the same bouncing light pulse clock installed on a moving train from a stationary frame.

Part 2 - Bob on the Ground: The second part of the thought experiment is to synchronize the bouncing light pulse with a clock stationary on the ground. This part consists of the following:

Bob stays on the ground.
Bob holds a clock which is fixed to the ground.
Bob uses the ground as his frame of reference x'.
Bob observes that the light pulse travels a diagonal upward path from the meter to the mirror and a diagonal downward path from the mirror to the meter. Both paths are having the same length L'.
Bob also observes that the light pulse takes T' seconds on his clock to complete a single round trip of bouncing.
Bob believes the special theory of relativity, and assumes the light pulse travels at the speed of light c in his frame.
Bob a relation between the elapsed time of T' seconds on his clock with the distance L' meters using the speed of light c: 2*L' = c*T'.
Bob declares that the Amy's bouncing light pulse is synchronized with his clock stationary clock on the ground. Each time the light pulse completes a single round trip of bouncing, his clock moves T' seconds.

Based on Bob's observations in his frame, we can derive a formula to express time T' in terms of distance L':

2*L' = c*T'                   (T.3) - Bob's observation
  # Light pulse speed, time and distance relation

T' = 2*L'/c                   (T.4) - moving variables around
  # Time on the stationary clock in Bob's frame

Notice that T' also represents the elapsed time observed by Bob between the same two events: event A when the light pulse is leaving the meter, and event B when the same light pulse is returning to the meter reflected back from the mirror.

If we compare Amy's observation and Bob's observation, we will get the following conclusion:

2*L = c*T                     (T.1) - Amy's observation
2*L' = c*T'                   (T.3) - Bob's observation
L' > L                        (T.5) - diagonal vs. vertical path
   # Diagonal path is longer than vertical path

2*L' > 2*L                    (T.6) - multiplying T.5 by 2
c*T' > c*T                    (T.7) - merging T.1 and T.3 into T.6
T' > T                        (T.8) - removing c from T.7
   # Elapsed time on moving clock is less than stationary clock

Congratulations, we have demonstrated the time dilation phenomenon. Bob observed a greater value T' of the elapsed time from his stationary frame between event A and event B.

Since event A and event B represents two consecutive clicks of the bouncing light pulse clock, we can say that Bob's clock is faster than the bouncing light pulse clock. Faster clocks produce greater elapsed time values than slower clocks between two given events.

Or we can say that bouncing light pulse clock in the moving frame is slower.

We can also say that Amy's clock in the moving frame is slower, since her clock is synchronized with the bouncing light pulse clock.

Time Dilation Demonstration - Bob on Ground

To see how much slower the moving clock is comparing with the stationary clock, continue with the third part of the thought experiment in the next section.