Demonstration of Length Contraction

∟Length Contraction in Special Relativity

∟Demonstration of Length Contraction

This section provides a thought experiment to demonstrate length contraction using a laser meter to observe and calculate the length of a carriage on a moving train from two different frames of references.

The most common way to demonstrate length contraction is to follow a thought experiment using a moving train with a carriage:

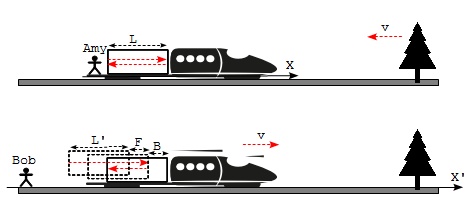
1. Have Amy performing the experiment on the moving train using the train as the frame of reference:

Amy installs a laser meter on the back wall of the carriage and a mirror on the front wall of the carriage.
Amy releases a laser light pulse from the meter, and waits for the pulse to be reflected back from the mirror.
Amy observes that it takes f seconds for the light pulse to travel forward from the meter to the mirror, and b seconds to travel backward from the mirror to the meter.

If Amy uses L as the length of the carriage and T as the total time for the light pulse to return to the meter, she will get the following formulas:

L = c*f                       (L.1) - Forward time-distance relation
L = c*b                       (L.2) - Backward time-distance relation
T = f + b                     (L.3) - Total time traveled in frame x
T = L/c + L/c                 (L.4) - Merge L.1 and L.2 into L.3
T = 2*L/c                     (L.5) - Combine two terms

L = c*T/2                     (L.6) - Normalize on L
   # Carriage length observed by Amy in frame x

2. Have Bob watching light pulse traveling forward in Amy's experiment on the ground using the ground as the frame of reference:

Bob observes that when the light pulse travels forward from the meter to the mirror, it traveled a distance longer than the length of the carriage, because the mirror is moving forward at the same time.
Bob observes that it takes f' seconds for the light pulse to travel forward from the meter to the mirror.

If Bob uses L' as the length of the carriage and F as the distance moved by the train within f' seconds, he will get the following formulas:

L' + F = c*f'                 (L.7) - Forward time-distance relation
F = v*f'                      (L.8) - Distance moved by the train
L' + v*f' = c*f'              (L.9) - Merge L.8 into L.7

f' = L'/(c-v)                (L.10) - Normalize on f'
   # Forward travel time observed by Bob in frame x'

3. Have Bob watching light pulse traveling backward in Amy's experiment on the ground using the ground as the frame of reference:

Bob observes that when the light pulse travels backward from the mirror to the meter, it traveled a distance shorter than the length of the carriage, because the meter is moving forward at the same time.
Bob observes that it takes b' seconds for the light pulse to travel backward from the mirror to the meter.

If Bob uses B as the distance moved by the train within b' seconds, he will get the following formulas:

L' - B = c*b'                (L.11) - Backward time-distance relation
B = v*b'                     (L.12) - Distance moved by the train
L' - v*b' = c*b'             (L.13) - Merge L.12 into L.11

b' = L'/(c+v)                (L.14) - Normalize on b'
   # Backward travel time observed by Bob in frame x'

4. Have Bob calculating the total travel time and carriage length:

If Bob uses T' as the total time for the light pulse to return to the meter, he will get the following formulas:

T' = f' + b'                 (L.15) - Total time traveled in frame x'
T' = L'/(c-v) + L'/(c+v)     (L.16) - Merge L.10 and L.14 into L.15

T' = L'*(1/(c-v) + 1/(c+v))  (L.17) - Taking L' out of two terms

T' = L'*((c+v)/(c**2-v**2) + (c-v)/(c**2-v**2))
                             (L.18) - Create same denominator

T' = 2L'*c/(c**2-v**2)       (L.19) - Combine two terms
T' = 2L'/(c*(1-v**2/c**2))   (L.20) - Normalize denominator

L' = (1-(v/c)**2)*c*T'/2     (L.21) - Normalize on L'
   # Carriage length observed by Bob in frame x'