Physics Notes - Herong's Tutorial Notes - v3.25, by Herong Yang
Formula for the Relativity of Simultaneity
This section provides a thought experiment to derive the formula for the relativity of simultaneity.
To derive the formula for the relativity of simultaneity, let's use a thought experiment based on the example given in the previous section.
Part 1 - Amy on the Train: The first part of the thought experiment is to establish two simultaneous events in a moving reference frame. This part consists of the following:
- Amy stays on a train that is moving at a speed of v relative the ground.
- Amy sets off a light at the center of the carriage when her clock reads 0 second.
- Amy observes light pulses travel at the speed of c.
- Amy uses the train as her frame of reference x.
- Assuming the total length of the carriage is L meters, Amy observes that the elapsed time of light pulses reaching to the back wall and the front wall is the same: 0.5*L/c.
If we let A and B be elapsed times of light pulses reaching the back wall and the front wall on Amy's clock, her observation can be expressed as:
A = 0.5*L/c (S.1) - time when light reaching the back B = 0.5*L/c (S.2) - time when light reaching the front B - A = 0 (S.3) - reaching walls simultaneously # Amy's observation in the moving frame
Part 2 - Bob on the Ground: The second part of the thought experiment is to observe the same events in a stationary reference frame. This part consists of the following:
- Bob stays on the ground.
- Bob synchronize his clock to 0 second when Amy sets off the light.
- Bob uses the ground as his frame of reference x'.
- Bob observes that the backward light pulse travels at the same speed of c and reaches the back wall with less time comparing to Amy's observation, because the back wall moved forward with a distance of E.
- Bob also observes that the forward light pulse travels at the same speed of c and reaches the front wall with more time comparing to Amy's observation, because the front wall moved forward with a distance of F.
If we let A' and B' be elapsed times of light pulses reaching the back wall and the front wall on Bob's clock, his observation can be expressed as:
A' = (0.5*L-E)/c (S.4) - Time when light reaching the back
B' = (0.5*L+F)/c (S.5) - Time when light reaching the front
E = A'*v (S.6) - distance moved by the back wall
F = B'*v (S.7) - distance moved by the front wall
A' = (0.5*L-A'*v)/c (S.8) - merging S.6 into S.4
B' = (0.5*L+B'*v)/c (S.9) - merging S.7 into S.5
A'*c + A'*v = 0.5*L (S.10) - moving variables in S.8
B'*c - B'*v = 0.5*L (S.11) - moving variables in S.9
A' = 0.5*L/(c+v) (S.12) - moving variables in S.10
B' = 0.5*L/(c-v) (S.13) - moving variables in S.11
B'-A' = 0.5*L/(c-v) - 0.5*L/(c+v)
(S.14) - difference between B' and A'
B'-A' = 0.5*L*(1/(c-v) - 1/(c+v))
B'-A' = 0.5*L*((c+v)/(c**2-v**2) - (c-v)/(c**2-v**2))
B'-A' = 0.5*L*((c+v) - (c-v))/(c**2-v**2)
B'-A' = 0.5*L*(2*v)/(c**2-v**2)
B'-A' = L*v/(c**2-v**2) (S.15) - reaching walls at different times
# Bob's observation in the stationary frame
Conclusion, two simultaneous events in Amy's frame observed as non-simultaneous in Bob's frame that is moving relatively.
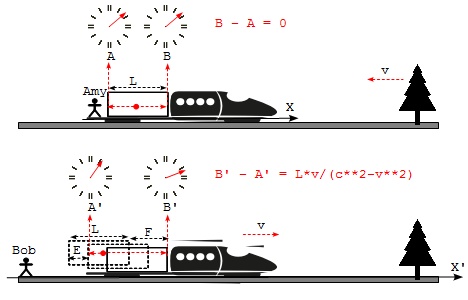
Table of Contents
Introduction of Frame of Reference
Introduction of Special Relativity
Time Dilation in Special Relativity
Length Contraction in Special Relativity
►The Relativity of Simultaneity
What Is the Relativity of Simultaneity
►Formula for the Relativity of Simultaneity
Minkowski Spacetime and Diagrams
Introduction of Generalized Coordinates